0、前言
文[1]-[6]对椭圆的切线与法线的性质进行了全面细致的研究,得到了一系列有趣的结论。本文将对椭圆的切线和法线有关的三个轨迹问题展开新的探索,发现了三条优美对称的高次曲线(切垂线、法垂线及法中线)和相关长度、距离公式,最后得到了与法垂线、法中线密切关联的椭圆曲星线(即渐屈线)、曲星圆和椭圆(法中线的外切椭圆)的优美性质。
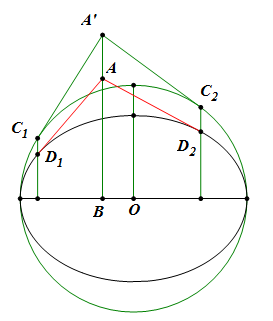
过椭圆上任一点,可以作它在该点处的切线和法线,其中法线总与椭圆相交,法线被椭圆截下的线段叫做该椭圆的法弦。

当m、n之一为0时,上列切线方程和法线方程仍然有效。
因此,椭圆在点P处的切线方程和法线方程分别为
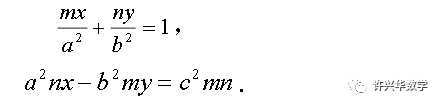
1、椭圆的切垂线
下面,我们以上述引理为依据,对与椭圆的切线和法线有关的轨迹问题进行全面而深入的探究。



图形如图2所示,蛮漂亮哦,好像一朵幸运的四瓣玫瑰花,但它是一条新发现的六次曲线,并不是大家熟悉的四叶玫瑰线。由于该曲线是椭圆中心向其法线所作垂线的垂足H的轨迹,故称之为椭圆的法垂线。
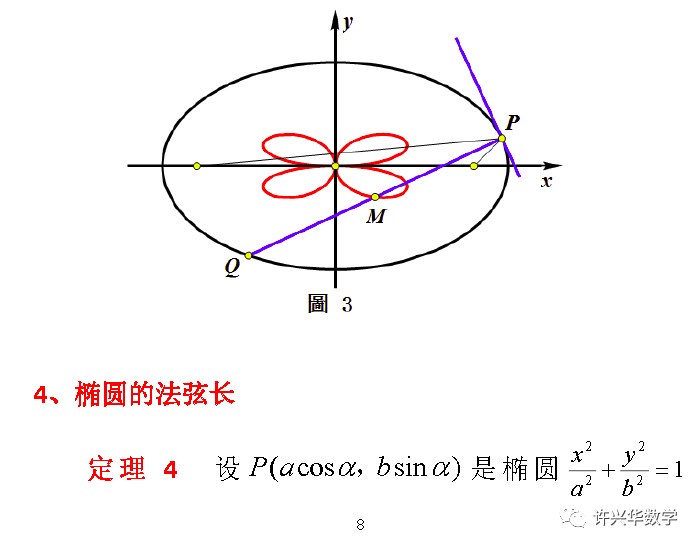
3、椭圆的法中线


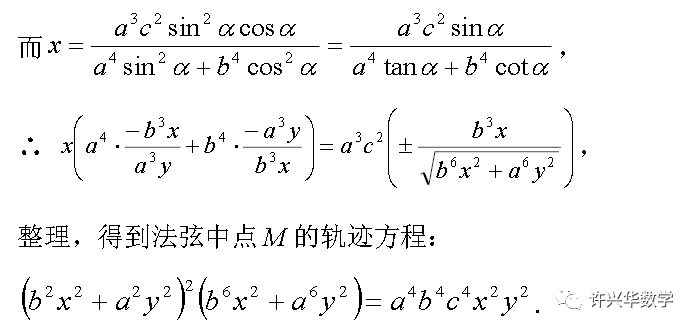
很明显,上列中点轨迹方程比定理1、2中的垂足轨迹方程要复杂,其图形如图3所示。由于该六次曲线是椭圆法弦中点M的轨迹,故称之为椭圆的法中线。


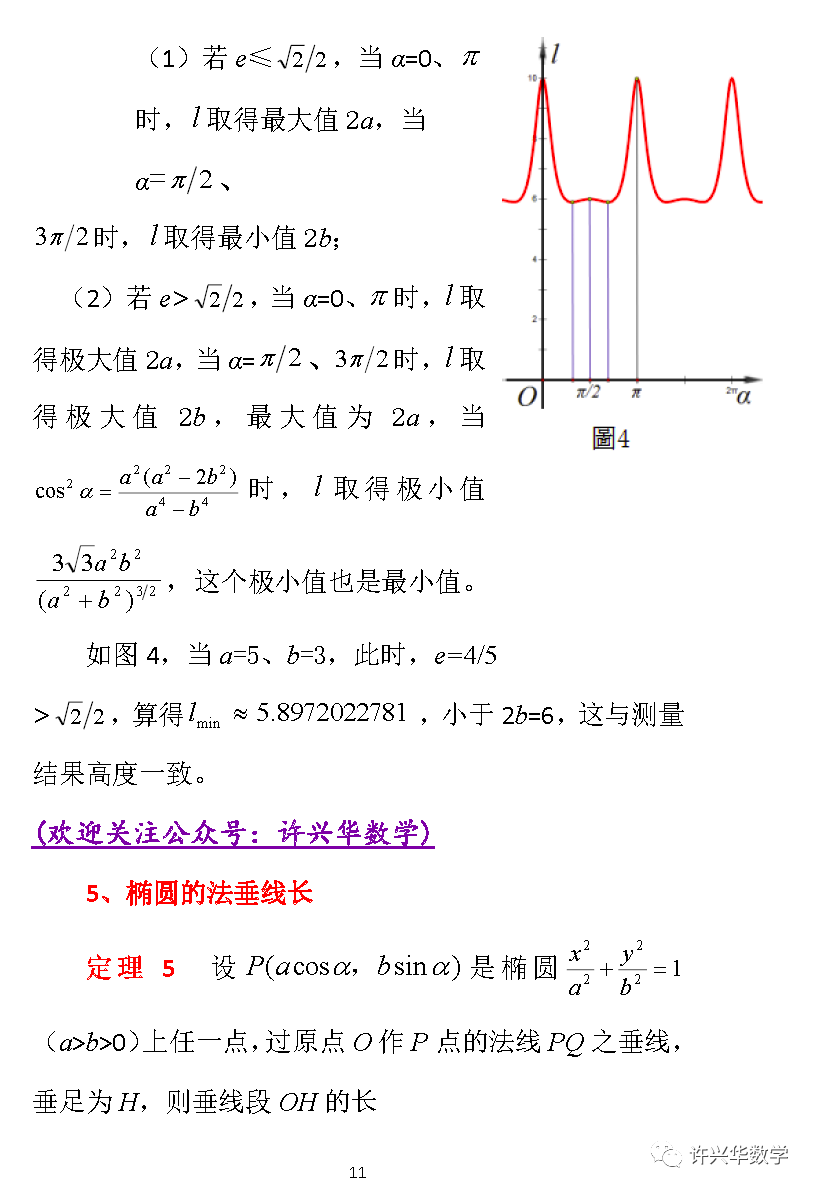


6、椭圆的曲星线、曲星圆和椭圆
如图5,称过原点作法线的垂线的垂足轨迹为椭圆的法垂线,法弦中点轨迹为椭圆的法中线。由于椭圆的渐屈线(曲率圆心轨迹)是其法线族的包络线,立得如下有趣结论
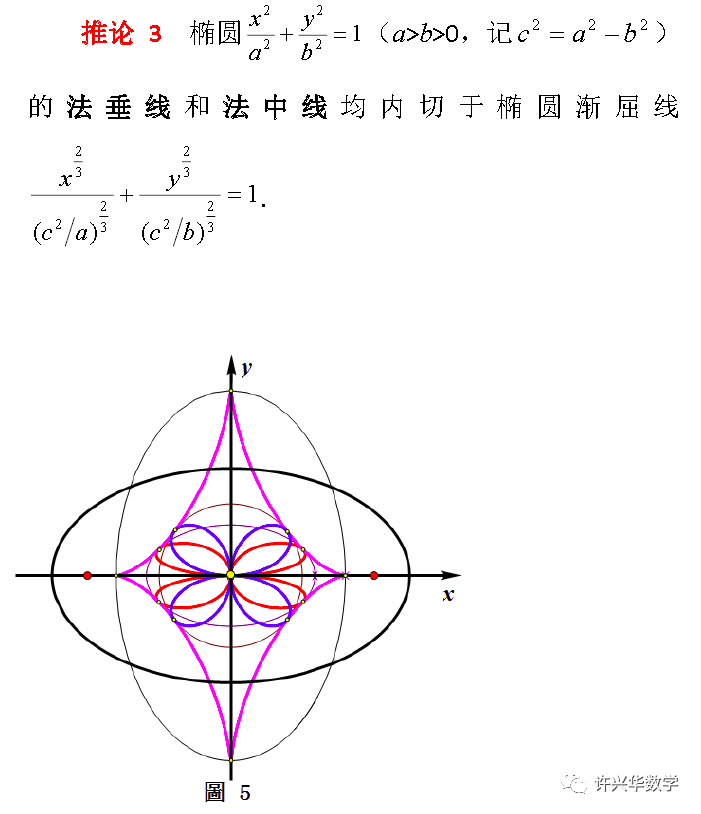
这条曲线是大家熟知的,考虑到椭圆渐屈线是其曲率中心的轨迹,酷似星星,不妨称之为椭圆的曲星线,称曲星线的内切圆为原椭圆的曲星圆。易得如下


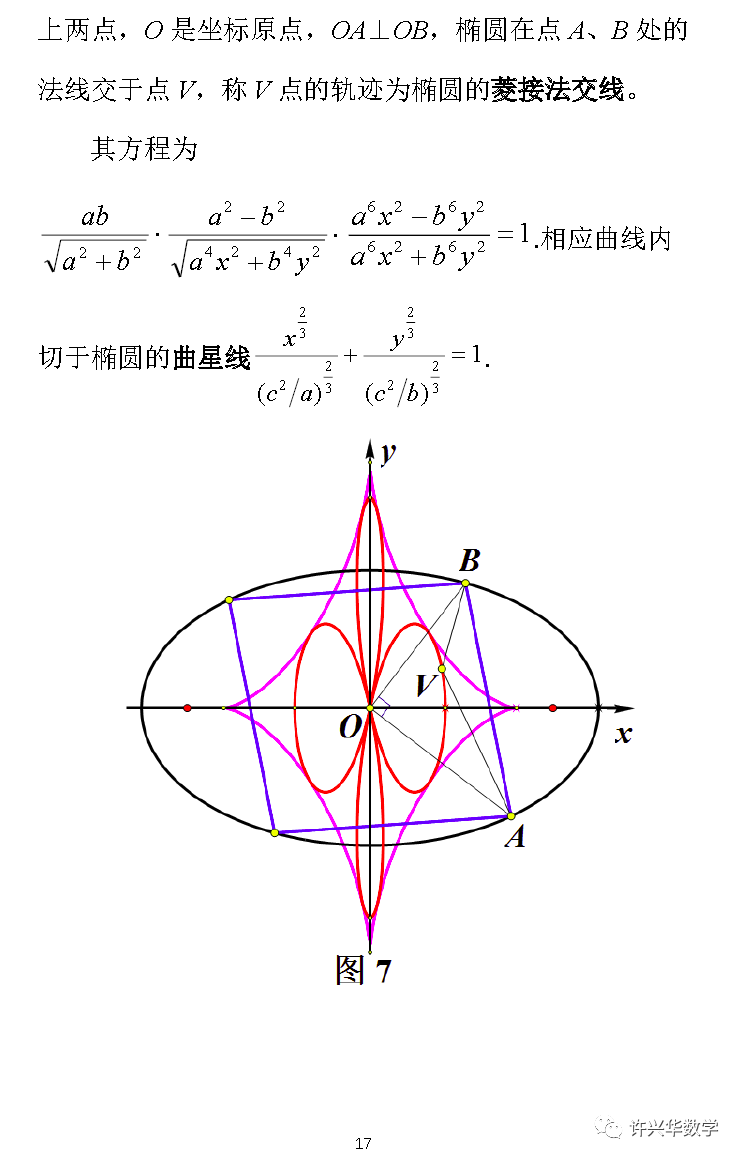
上述推论3-11的证明较繁,此处从略,拟另文介绍。
自然地,我们可以对双曲线、拋物线进行同样的探讨,得到类似结论。限于篇幅,这里不赘,留给感兴趣的读者。
【参考文献】
1、杜林会,椭圆切线的几个性质及作法[J],数学通报,2003(6)
2、周建华,圆锥曲线切线的一个有趣的性质[J],数学通报,2003(12)
3、杨波,有心圆锥曲线的一个性质及应用[J],数学通报,2005(3)
4、徐文春,关于有心圆锥曲线切线的一组性质[J],数学通讯,2012(12)
5、曾建国,有心圆锥曲线切线的一个性质的推广[J],数学通讯,2013(5)
6、杨志明,一个关于有心圆锥曲线切线的猜想的否定与修正[J],数学通讯,2013(10)

【投稿须知】公众号《许兴华数学》诚邀全国各地中小学数学教师、教研员和数学爱好者热情投稿!来稿时请注意以下五点:
1、本站发布的内容部分购买于网络,仅供读者学习与参考,如有侵权,请联系站长进行删除处理。
2、本站一切资源不代表本站立场,不代表本站赞同其观点和对其真实性负责。
3、本站仅分享资源,以极低的价格降低大家被割韭菜的损失。本站无法保证资源质量,所以介意的小伙伴请勿下单!
4、资源大多存储在云盘,如发现链接失效,请联系站长第一时间更新。