十平方米等于多少平方分米-小学六年级数学小升初必会的典型题+答案和解题思路，收藏多练习，考试不丢分！

小升初数学必会的典型题解题思路

1.下图是一张长方形纸折起来后的图形。已知∠1=30°，∠2的度数是多少？

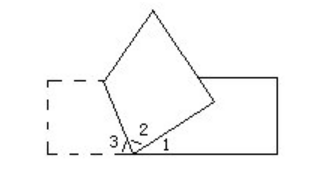
思路：若把折起来的纸打开，就可以看到∠1、∠2和∠3组成一个平角，而∠2和∠3相等。

解：∠2=（180°-30°）÷2＝75°

答：∠2的度数是75°。

2.根据三角形内角和是180°，你能求出下面的四边形和正六边形的内角和吗？

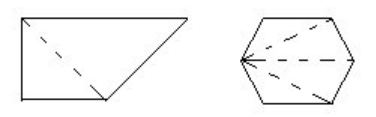
思路：（1）四边形可以分成2个三角形，因为一个三角形的内角和是180°，可求四边形的内角和。

解：180°×2＝360°

思路：（2）正六边形可以分为4个三角形，一个三角形的内角和是180°，可求正六边形的内角和。

解：180°×4=720°

3.下图中大平行四边形的面积是48平方厘米。A、B是上、下两边的中点。你能求出图中小平行四边形的面积吗？

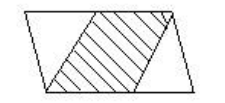
思路：因为A、B分别是上、下两条边的中点，所以这个小平行四边形的底边形的一半。

解：48÷2=24（平方厘米）。

答：小平行四边形面积是24平方厘米。

4.一张边长4厘米的正方形纸，从一边中点到邻边的中点连一条线段，沿这线段剪去一个角，剩下的面积是多少？

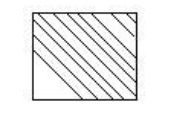
解：4×4—（4÷2）2÷2＝14（平方厘米）

答：剩下的面积是14平方厘米。

5.已知右面梯形的上底是20厘米，下底是34厘米，其中阴影部分的面积是340平方厘米。求这个梯形的面积是多少？

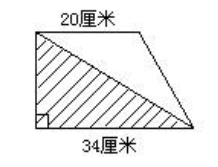
思路：阴影部分是一个直角三角形，它的面积和底已知，可以先求出这个三角形的高，也就是这个梯形的高，然后根据梯形面积公式求出梯形的面积。

解：

高：340÷34×2=20（厘米）

面积：（20＋34）×20÷2＝540（平方厘米）

答：这个梯形的面积是540平方厘米。

6.在下面的梯形中，剪下一个最大的三角形，剩下的是什么图形？剩下的图形的面积是多少平方厘米？

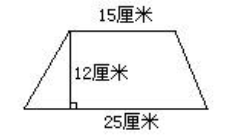
思路：以下底为底，以上底上一点为三角形的顶点剪下的三角形都是面积最大的。因为所有的三角形的底和高都没有变。剩下的图形可能是一个三角形，也可能是两个三角形。

解：15×12÷2=90（平方厘米）

答：剩下的面积是90平方厘米。

7.在图中，梯形的面积是72平方厘米，请你算出阴影部分的面积。

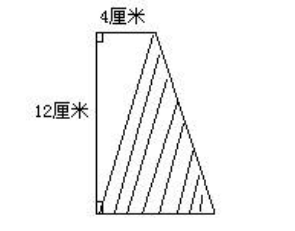
思路：阴影部分是一个三角形，这个三角形的面积是梯形的面积减去空白三角形面积的差，所以先算空白三角形的面积。

解：72—12×4÷2＝48（平方厘米）

答：阴影面积是48平方厘米。

8.计算下图的面积，你能想出不同的解法吗？

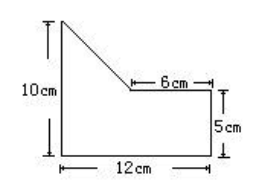
思路：（1）用一个长方形的面积加上一个三角形的面积。

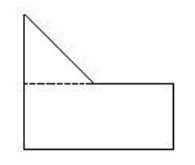
解：（1）12×5＋（12—6）×（10—5）÷2＝75（平方厘米）

思路：（2）用一个梯形的面积加上一个长方形的面积。

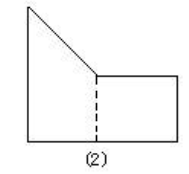
解：（2）（5＋10）×（12—6）÷2＋5×6=75（平方厘米）

思路：（3）用一个三角形面积加上一个梯形面积。

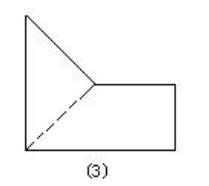
解：10×（12—6）÷2＋（6＋12）×5÷2=75（平方厘米）

思路：（4）用一个大长方形的面积减去一个梯形的面积。

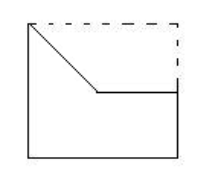
解：12×10-（6＋12）×（10—5）÷2=75（平方厘米）

9.下面的竖式中的字母a、b、c、s、t各代表什么数？

思路：被减数是五位数，减数是四位数，差是三位数，可立即确定被减数万位上的a代表1，减数千位上的S代表9，又因为做加、减法时是从个位起依次计算的，可从右到左依次确定t＝6，c＝0，b=5。

解：a＝1 b=5 c＝0 s＝9 t＝6

10.在下面的竖式中，a、b、c、s各代表什么数字？

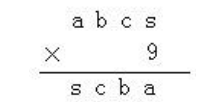
思路：一个四位数乘以9，积仍是四位数，所以a只能是1，s只能是9。因为b乘以9不能进位。b又不可能等于1，所以b只能是0。再根据积的十位是0，由c乘以9加进上来的8得出的个位数字可推出c乘以9的积的个位数字是2，就不难想出c＝8。

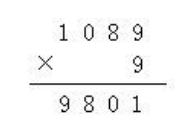
解：a＝1 b＝0 c＝8 s＝9

11.已知a和b都是自然数，并且a＋b＝100。a和b相乘的和，最大可以是多少？最小可以是多少？

解：当a=50，b＝50时

a×b＝50×50＝2500。

当a＝99，b＝1时

a×b＝99×1=99。

答：最大是2500，最小是99。

12.下图是一个等边三角形。已知∠1=∠2，∠3=∠4，X的度数是多少？

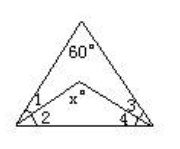
思路：根据三角形内角和是180°，∠2＋∠4＋X°=180°，又因为∠1=∠2，所以由等边三角形推出∠1=∠2=60°÷2＝30°，同理得出∠3=∠4＝30°。

解：180°-（60°÷2）×2＝120°

答：X的度数是120°。

13.早晨小明和爸爸、妈妈一起跑步。爸爸跑的路程比小明的2倍少20米，比妈妈的2倍多10米。小明和他妈妈谁跑的路程长一些？

思路：从第一个条件可判断小明所跑路程的2倍比爸爸跑的路程长，从第二个条件可判断妈妈所跑的路程的2倍比爸爸跑的路程短。由上面两个判断可推出小明跑的路程的2倍比妈妈跑的路程的2倍长。也就是小明比妈妈跑的路程长。

解：小明比妈妈跑的路程长。

14.两地间的公路长480千米。两辆汽车同时从这两地相对开出，甲车的速度是乙车的2倍，4小时相遇。两车每小时各行多少千米？

解：设乙车的速度为x千米，则甲车的速度为2x千米。

（x＋2x）×4＝480

x＝40

40×2＝80（千米）

答：甲速为80千米，乙速为40千米。

15.一个长方形的周长是30厘米，长是宽的2倍。求这个长方形的面积。

思路：先求宽，再求出长，最后求面积。

解：设宽为x厘米。

（2x＋x）×2=30

x＝5

5×2＝10（厘米）

5×10＝50（平方厘米）

答：这个长方形面积是50平方厘米。

16.箱子里装有同样数目的乒乓球和羽毛球每次取出5个乒乓球和3个羽毛球，取了几次以后，乒乓球没有了，羽毛球还剩6个。一共取了几次？乒乓球和羽毛球各有多少个？

思路：两种球的数目相等，乒乓球取完时，羽毛球还剩6个，说明乒乓球多取了6个，而每次乒乓球多取2个，可见一共取了6÷（5-3）次。再求两种球各有多少个。

解：

（1）一共取的次数

6÷（5—3）=3（次）

（2）乒乓球的个数

5×3＝15（个）

（3）羽毛球的个数

3×3＋6＝15（个）

答：乒乓球和羽毛球各15个。

17.一个三位数，它能被2整除，又有约数5，百位上的数是最小的质数，十位上的数是百位上的数的倍数。这个三位数可能是多少？

思路：从前两个条件可得这个数的个位是0，从百位上的数是最小的质数得出百位上是2，从十位上的数是百位上的数的倍数可得出这个三位数可能是220、240、260和280。

解：这个三位数可能是220、240、260和280。

18.有三根木棒，分别长12厘米、44厘米、56厘米。要把它们都截成同样长的小棒，不许剩余，每根小棒最长能有多少厘米？

思路：每根小棒的长度必须能整除12、44、56，否则就会有剩余。因为要求最长的小棒，所以就是求12、44、56的最大公约数。

解：每根小棒最长能有4厘米。

19.有三个质数，它们的乘积是1001，这三个质数各是多少？

思路：就是把1001分解质因数。

1001＝13×11×7。

解：这三个质数是13、11和7。

20.有一张长方形纸，长70厘米，宽50厘米，如果要剪成同样大的小正方形。这些小正方形的边长最大可能是多少厘米？

思路：根据题意，边长最大，也就是求70和50的最大公约数。因为70和50的最大公约数是10。

解：这个小正方形边长最大可能是10厘米。

21.一排电线杆，原来每根之间的距离是30米，现在改为45米，如果起点的一根电线杆不移动，至少再隔多远又有一根电线杆不移动？

思路：原来每根电线杆到起点那一根的距离都是30的倍数，而现在每根电线杆到起点那一根的距离都是45的倍数，要知道和起点那一根电线杆至少相隔多少个30米和45米的电线杆不必移动，就要求出30和45的最小公倍数。即90米处的那一根不用移动。

解：第三根及3的倍数的电线杆不移动。

22.有同样大小的红、黑、白玻璃球共73个。按1个红球、2个黑球、3个白球的顺序排列着。三种颜色的玻璃球各占总数的几分之几？第68个玻璃球是什么颜色的？

思路：每1个红球、2个黑球、3个白球看作一组，在每组6个球中，第一个是红球、第2、3个是黑球，第4、5、6个是白球。要求出这三种颜色的玻璃球各占总数的几分之几？先要求73个玻璃球中红、黑、白各有多少个。要求出各有多少个，先算一下73个球可分几组。

73÷6=12（组）……1（个）

也就是说，这73个球被分成12组后还余下1个，这余下的1个球应该是红球。

解：（1）红球：1×12＋1＝13（个）

（2）黑球：2×12=24（个）

（3）白球：3×12＝36（个）

而68÷6＝11（组）……2（个），余下的2个球按顺序第1个是红的，第2个是黑的，所以第68个球是黑颜色的。

23.从正午12时时针与分针相遇，到午夜12时，时针与分针还能相遇多少次？

思路：从12时以后，时针每走过一个数与分针相遇一次，如时针刚走过数1，与分针第一次相遇，以下以此类推。当时针和分针都快接近11时，两针第10次相遇，接着在午夜12时第11次相遇。

解：共11次相遇。

24.有两只水桶，一只可装水7千克，另一只可装水5千克，现在只用这两只水桶量水，请你想一想，怎样能量出1千克水呢？

解：先用5千克水桶量出5千克水，倒入7千克水桶中，再用5千克的水桶量出5千克水倒入已装水5千克的7千克水桶，这时5千克水桶里剩下3千克水，将7千克水桶中的水倒掉，把5千克水桶中的3千克水倒入7千克水桶中，再用5千克水桶量出5千克水，倒满已装3千克水的7千克水桶，剩下的就是1千克水。

25.下面这个分数的分子、分母是由1～9九个数字组成的。你能把它约成最简分数吗？

思路：先用3去约分，约分后的分母是原分数的分子，说明原来的分子、

26.学校买来三种新书共100本。其中文艺书是科技书的3倍，画册比科技书的一半还少8本。这三种书各买了多少本？

思路：设科技书有x本，文艺书是3x本，画册就有（0.5x-8）本。

解：设科技书有x本。

x＋3x＋0.5x-8=100

x＝24

24×3＝72（本）

24×0.5-8＝4（本）

答：科技书有24本，文艺书有72本，画册有4本。

剩下的几个数字，能否再组成两个与它等值的分数。

28.有1、2、3、4数字卡片各一张，每次取两张组成一个两位数，可以组成多少个偶数？

思路：当2放在个位上时组成的两位数有3个：12、32、42，当4放在个位上时，组成的两位数有3个：14、24、34。

解：可以组成六个偶数。

29、

30、

31、

33、

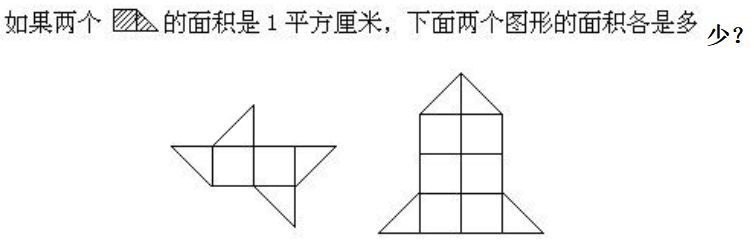
34、

35.把6个同样大小的苹果平均分给8个孩子，每个孩子都分得一大块和一小块。是怎样分的？每个孩子分得多少？

36.在下面的○里填上适当的数，使每个正方形四个角上的数加起来等于1。

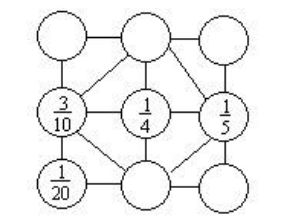
解：见下图。

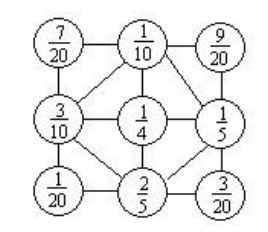
37.在○里填上适当的运算符号，在□里填适当数字。

38.先计算下面各题，然后找出规律。

解：后一个加数的分母是前一个加数分母的2倍，分子都是1，和的分母与最后一个加数的分母相同，分子比分母少1。

39、

40、

秦华和王英比，谁高一些，高多少米？

41、

42.右面正方形是由七巧板拼成的，每个图形是正方形的几分之几？图形7和4共占正方形的几分之几？图形3、4和5呢？

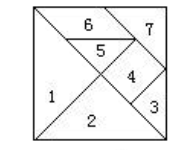
43、

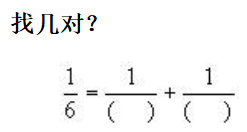
思路：根据分数的基本性质和加、减法的关系来推理。

44.你能很快算出下面的算式等于多少吗？

思路：分母相同，分子是从1～19的连续十个奇数的和，根据等差数列求和公式（首项+末项）×项数÷2可得分子的和。

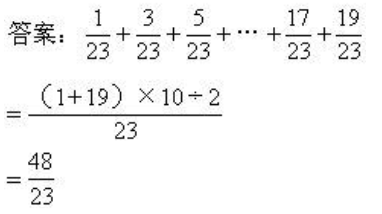
思路：（1）先求获一等奖的占总人数的几分之几，再从获一、二等奖的共占获奖的总人数的几分之几中减去获一等奖的部分，就得获二等奖的部分。

思路：（2）先求获三等奖的占获奖总人数的几分之几，再从获二、三等奖的共占获奖总人数的几分之几中减去获三等奖的部分，得到获二等奖的部分。

46、

思路：因为一共运来5箱苹果，从剩下的苹果正好等于原来的2箱的重量，可推出卖出的苹果正好是原来的3箱的重量。卖出的重量除以3就是原来每箱的重量。

答：原来每箱苹果20千克。

47.用1、4、5三个数字组成两个带分数使下面的等式成立（每个带分数都由1、4、5三个数组成）。

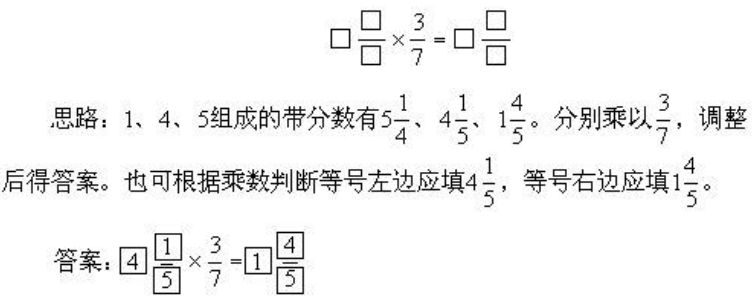
48.用5个3组成一个算式，要使算式中至少有一个分数，得数分别等于0、1、2、3。

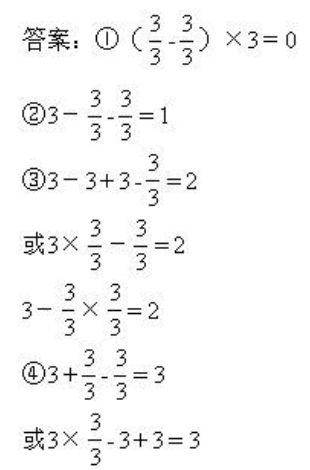
50、

51、

52、

53.先计算前两个算式，再填出第三个算式的得数。

54、

思路：先求2筐橙子的重量，再求水果的重量，最后求香蕉的重量。

答：售出香蕉22千克。

55、

56、

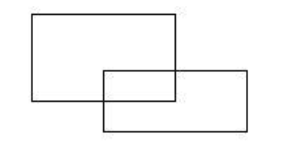
思路：先求大长方形面积含多少个重叠的部分的面积，再求小长方形面积，最后求大，小长方形面积的比。

答：大小长方形面积比是3∶2。

57、

答：乙袋原来装米30千克。

58、

59.用绳子测井深，把绳三折来量，井外余16分米，把绳子四折来量，井外余4分米。求井深和绳长。

解：解：设绳长x分米。

x＝144

61.一段公路，甲队单独修要15天，乙队单独修要12天。甲、乙两队从这段公路的两端同时合修3天后，还相距3.52千米。这段公路长多少千米？

思路：先求甲乙两队合修3天后完成的分率，再求这段公路的全长。

答：这段公路的全长是6.4千米。

62.同学们参加野营活动。一个同学到负责后勤的老师处领碗，老师问他领多少，他说：“领55个。”又问：“多少人吃饭？”他说：“一人一个饭碗，两人一个菜碗，三个人一个汤碗”算一算这个同学给多少人领碗？

思路：“一人一个饭碗，两人一个菜碗，三个人一个汤碗”，可以看作是，

解：设给x个人领碗。

x＝30

答：给30个人领碗。

63.一个带盖的长方体水箱，体积是0.576立方米。它的长是12分米，宽是8分米。做这样一个木箱至少要用木板多少平方米？

思路：先求长方体的高，再求它的表面积。

解：0.576立方米=576立方分米。

576÷12÷8＝6（分米）

（12×6＋6×8＋12×8）×2＝432（平方分米）

432平方分米=4.32平方米。

答：至少要用木板4.32平方米。

64.一个长方体房间，长5.2米，宽3米，高2.6米。它的四面墙的下部涂31.10米高的浅绿色油漆，涂油漆的面积有多少平方米？四面墙壁的上部和房顶粉刷白色涂料（门、窗面积8平方米不刷），粉刷白色涂料的面积有多少平方米？

解：（5.2×1.1+3×1.1）×2=18.04（平方米）

［5.2×（2.6-1.1）＋3×（2.6—1.1） ］×2＋5.2×3-8

=32.2（平方米）

答：涂油漆面积是18.04平方米，刷白色涂料的面积是32.2平方米。

66.有两缸金鱼，如果从第一缸里取出15尾放入第二缸里，这时第二缸

的金鱼比第二缸里原有的金鱼多多少尾？

思路：从第一缸里取出15尾放入第二缸后，第二缸多了15尾，而第一缸少了15尾。根据第二个条件的等量关系列方程求出第一缸的金鱼数再求出题中的问题。

解：设第一缸里原有金鱼x尾。

x=85

85—35＝50（尾）

答：第一缸原有的比第二缸原有的多50尾。

67.一辆自行车轮胎的外直径约是71厘米，如果平均每分钟转100周，通过一座长1099米的桥，大约要用几分钟？

思路：先求外轮胎的周长，再求每分钟自行车所走的路程，最后求大约用的时间。

解：1099÷（71×3.14×100÷100）≈5（分）

答：大约要用5分钟。

68.在一个正方形里，分别以两条对边为直径画两个半圆（如图），知道其中一个半圆的半径是3厘米，求图中阴影部分的面积。

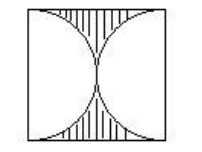
思路：用正方形的面积减去2个半圆的面积，把正方形的2个半圆旋转之后成为一个整圆，那么阴影部分面积就是正方形面积减去一个圆的面积。

解：（3×2）- 3.14 ×3＝7.74（平方厘米）

答：阴影部分的面积是7.74平方厘米。

69.一个稻谷囤上面是圆锥形，下面是圆柱形。圆柱的底面周长是9.42米，高2米，圆锥高0.6米。每立方米稻谷约重550千克，这囤稻谷约重多少千克？（得数保留整百千克。）

思路：根据底面周长先求圆的半径，再用圆柱体的体积加上圆锥体的体积，最后求这囤稻谷的重量。

70.用白铁皮制作圆柱形通风管25节，每节长80厘米底面圆的周长是31.4厘米。问至少要白铁皮多少平方米（用进一法取值。）

思路：先求圆柱体的侧面积，再求25个圆柱体的表面积，注意单位换算。

解：31.4×80×25÷100≈7（平方米）

答：至少要用7平方米白铁皮。

71.有一个正方体木材，它的棱长是4分米，把这块木料加工成一个最大的圆柱体，这个圆柱体的体积是多少？

思路：正方体棱长为42分米，做成的最大的圆柱体的直径为4分米，高也是4分米。

解：3.14×（4÷2）×4＝50.24（立方米）

答：这个圆柱体的体积是50.24立方米。

72、一个机器厂原计划每天生产40台机器，20天可以完成。如果要提前4天完成，每天要完成原计划日产量的百分之几？

思路：先求20天生产的总台数，如果提前4天实际用的时间是20—4＝16（天），再求出实际工效，最后求每天完成计划日产量的百分率。

解：［40×20÷（20—4）］÷40×100％=125％

答：每天要完成原计划日产量的125％。

73、汽车运输场有大小货车 115 辆，大货车比小货车的 5 倍多 7 辆，运输场有大货车和小汽车各有多少辆？

分析：大货车比小货车的5 倍还多 7 辆，这 7 辆也在总数 115 辆内，为了使总数与（ 5+1 ）倍对应，总车辆数应（ 115-7 ）辆 。

列式为：

（115-7 ）÷（ 5+1 ） =18 （辆）

18×5+7=97 （辆）

答：运输场有大货车97辆，小汽车18辆。

74、甲乙两根绳子，甲绳长 63 米 ，乙绳长 29 米 ，两根绳剪去同样的长度，结果甲所剩的长度是乙绳 长的 3 倍，甲乙两绳所剩长度各多少米？各减去多少米？

分析：两根绳子剪去相同的一段，长度差没变，甲绳所剩的长度是乙绳的 3 倍，实比乙绳多（ 3-1 ）倍，以乙绳的长度为标准数。

列式：

（63-29）÷（ 3-1）=17（米）…乙绳剩下的长度，

17×3=51（米）…甲绳剩下的长度，

29-17=12（米）…剪去的长度。

75、某加工厂甲班和乙班共有工人 94 人，因工作需要临时从乙班调 46 人到甲班工作，这时乙班比甲班人数少 12 人，求原来甲班和乙班各有多少人？

分析：从乙班调 46 人到甲班，对于总数没有变化，现在把乙数转化成 2 个乙班，即 9 4 － 12 ，由此得到现在的乙班是：

（94－12）÷2=41 （人）

乙班在调出 46 人之前应该为：

41+46=87 （人）

甲班为 ：94－87=7 （人）

【福利领取：点击下方小程序即可免费学习】